Dijkstra's Shortest Path

Introduction

This is one of the most common algorithms that is used to get the shortest path from a single source point. This is useful since we can get the shortest distance to all the other points reachable from a single source point.

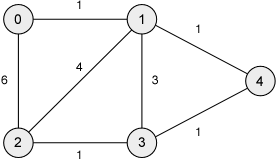
Lets see how this algorithm works,

let us start from the node 0

First we initiate all the nodes to distance infinity while having the starting node at distance 0, which is obvious.

from 0 we start traversal. Now we update the distances to the nearest node. Now distances are as follows

to 1 = 1
to 2 = 6
to 0 = 0

since we already covered 0 we no more consider it in our algorithm

For the shortest path to any node we should have the shortest path to every other node. So what we have to do is continue the previously done procedure ahead. Now take the node with the minimum distance node, which is 1 which has a distance 1 from 0. Update its neighbours now. The once that are not covered. Now

to 2 = 1(distance to 1) + 4 (distance 1 to 2) = 5
so now we have updated the node 2
continuing the same the final result,
to 0 = 0 covered
to 1 = 1 covered
to 2 = 5
to 3 = 4
to 4 = 2

Now we continue the procedure for node 4 and update node 3 to be distance 3 (2 + 1). This continues with the remaining node 3 and 2 but the results don't change here since we already have the optima. This is a dynamic programming approach, thus the results does not hold always true. This algorithm fails for negative edges. Because it'll keep one jumping between two nodes without ending or giving an erroneous output.

Program Code

This can be easily implemented in java as follows